Softmax regression (d2l)
Contents
12. Softmax regression (d2l)¶
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
import numpy as np
import matplotlib.pyplot as plt
from IPython import display
from d2l import torch as d2l
12.1. utils¶
def load_data_fashion_mnist(batch_size, resize=None, n_workers = 4): #@save
""" 讀 Fashion-MNIST 的 function
args:
- batch_size: 做 DataLoader 時要用的
- resize: 例如 (224, 224), 最一開始讀檔時,trans 要用的.
- n_workers
output:
- trainning 的 iterator 和 testing 的 iterator
"""
# transformation
trans = [transforms.ToTensor()] # transforms.ToTensor() 會把 PIL 物件(uint8, 0~255 int) 先轉成 float32, normalize 到 0~1 之間, 再轉成 tensor (channel first, 灰階是 1)
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
# dataset
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
# dataloader
train_loader = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers= n_workers)
test_loader = data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers= n_workers)
return (train_loader, test_loader)
def get_fashion_mnist_labels(labels): #@save
"""
原本的 label 是 0-9 的 int, 現在把他轉成 text labels
args:
- labels: list, 每個 element 都是 0-9 的 int
"""
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save
"""
args:
- imgs: tensor; shape = (batch_size, h, w) for 灰階; (batch_size, h, w, c) for RGB; 所以要先幫他轉成 channel last
- num_rows
- num_cols
"""
figsize = (num_cols * scale, num_rows * scale)
_, axes = plt.subplots(num_rows, num_cols, figsize=figsize)
axes = axes.flatten()
max_num_imgs = np.min([num_cols*num_rows, imgs.shape[0]])
for i, (ax, img) in enumerate(zip(axes, imgs[:max_num_imgs])):
if torch.is_tensor(img):
ax.imshow(img.numpy())
else:
# PIL圖片
ax.imshow(img)
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
if titles:
ax.set_title(titles[i])
return axes
12.2. 讀檔¶
batch_size = 32
train_iter, test_iter = load_data_fashion_mnist(batch_size)
X, y = next(iter(train_iter))
print(X.shape)
print(X.dtype)
print(X.min())
print(X.max())
torch.Size([32, 1, 28, 28])
torch.float32
tensor(0.)
tensor(1.)
y
tensor([4, 2, 4, 7, 1, 9, 7, 2, 5, 9, 7, 1, 8, 1, 5, 6, 7, 6, 2, 5, 8, 0, 5, 9,
8, 9, 9, 9, 8, 8, 4, 0])
get_fashion_mnist_labels(y)
['coat',
'pullover',
'coat',
'sneaker',
'trouser',
'ankle boot',
'sneaker',
'pullover',
'sandal',
'ankle boot',
'sneaker',
'trouser',
'bag',
'trouser',
'sandal',
'shirt',
'sneaker',
'shirt',
'pullover',
'sandal',
'bag',
't-shirt',
'sandal',
'ankle boot',
'bag',
'ankle boot',
'ankle boot',
'ankle boot',
'bag',
'bag',
'coat',
't-shirt']
畫個圖來看看
show_images(X.reshape(32, 28, 28), num_rows = 4, num_cols = 8, titles = get_fashion_mnist_labels(y));

12.3. from scratch¶
12.3.1. 定義模型¶
假設圖形拉成向量後是 p 維,然後 label 的 class 有 c 類,那從圖形的角度來理解 softmax,就是:
input層: p 個 neuron
第一層: c 個 neuron
output: 把 c 個 neruon 做 softmax,使其 c 個 output 值的加總為 1
用數學來表達的話(順便把 batch_size = n 也帶入),符號可定義為:
\(\mathbf{Y} \in \mathbb{R}^{n \times c}\), label 矩陣, n個樣本,每個樣本都是 1xc 的 one-hot encoding.
\(\mathbf{X} \in \mathbb{R}^{n \times p}\), 資料矩陣, n個樣本,每個樣本都是 1xp 的 vector (像素拉成向量)
\(\mathbf{W} \in \mathbb{R}^{p \times c}\), 權重矩陣,shape = (p, c),input p 個 neuron,ouput c 個 neuron
\(\mathbf{b} \in \mathbb{R}^{1\times c}\), bias 向量, shape = (1, c)
式子為:
softmax 是對 \(\hat{\mathbf{y}}\) 的每一列做,做完後,每一列所有element的加總為 1
來定義一下 softmax function
def softmax(X):
X_exp = torch.exp(X) # 每個 element 都先取 exp
partition = X_exp.sum(1, keepdim=True) # 對每一列取 sum
return X_exp / partition # 這裡用了 broadcasting
試試看:
X = torch.normal(0, 1, (2, 5))
X
tensor([[ 0.7939, -0.0138, 0.0116, -0.1706, 0.4581],
[-0.5037, 1.1059, 0.2747, -1.3178, 1.5509]])
X_prob = softmax(X)
X_prob
tensor([[0.3334, 0.1487, 0.1525, 0.1271, 0.2383],
[0.0609, 0.3045, 0.1326, 0.0270, 0.4751]])
X_prob.sum(1)
tensor([1.0000, 1.0000])
現在,可以來定義模型了:
def model(X, params):
""" softmax regression """
W, b = params
O = torch.matmul(X.reshape((-1, W.shape[0])), W) + b
Y_hat = softmax(O)
return Y_hat
12.3.2. loss function¶
假設 y 有 C 個 class,資料筆數為 n,那:
y 為 nxc matrix,每一列都是 one-hot encoding.
y_hat 為 nxc matrix,每一列是 c 個 class 的 predict probability
categorical cross entropy 被定義為: \(\frac{1}{n} \sum_{i=1}^n \left( - \sum_{j=1}^C y_{ij} log \hat{y_{ij}}\right)\)
其中,loss 就是中間那項 \(- \sum_{j=1}^C y_{ij} log \hat{y_{ij}}\),cost 是用 mean 來 summarise (你要用 sum 來 summarise 也可以)
一般來說,\(y_i\) 不是 one-hot encoding,就是 index encoding (e.g. 總共 c 類,那 y 的值域為 0 到 c-1),在這種情況下,index encoding 的計算方法比較簡單,他就挑 y = 1 的 y_hat 出來即可
但之後會慢慢接觸到,y 可能是 mix-up 的結果,也就是說, y 仍是 c 維 vector,只是它不是 one-hot 了,他是 c 個 probability.
那我們仍然可以用上面的定義去計算 cross entropy,此時的解釋,就會變成去看 y 和 y_hat 的 distributioin 像不像
現在,來自己寫兩個 loss function,一個給 one-hot encoding 用,一個給 index encoding 用:
class MyCategoricalCrossEntropy:
def __init__(self, reduction = "mean"):
self.reduction = reduction
def __call__(self, y_hat_mat, y_mat):
"""
args:
- y_hat_mat: shape = (batch_size, c), c = one_hot_vector_size
- y_mat: shape = (batch_size, c), c = one_hot_vector_size
"""
log_y_hat_mat = torch.log(y_hat_mat)
loss = y_mat*log_y_hat_mat
loss = -1*loss.sum(1)
if self.reduction == "mean":
cost = loss.mean()
if self.reduction == "sum":
cost = loss.sum()
if self.reduction == "none":
cost = loss
return cost
# instance
loss = MyCategoricalCrossEntropy(reduction = "none")
y_hat_logit_mat = np.array(
[[-2.3, 4, 1.5],
[-5, 2, 8]]
)
y_hat_logit_mat = torch.tensor(y_hat_logit_mat)
y_hat_mat = softmax(y_hat_logit_mat)
# y_hat_mat = np.array(
# [[0.2, 0.2, 0.6],
# [0.1, 0.8, 0.1]]
# )
y_mat = np.array(
[[0, 0, 1],
[0, 1, 0]]
)
y_hat_mat = torch.tensor(y_hat_mat)
y_mat = torch.tensor(y_mat)
loss(y_hat_mat, y_mat)
<ipython-input-127-90f11e6105ed>:19: UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).
y_hat_mat = torch.tensor(y_hat_mat)
tensor([2.5806, 6.0025], dtype=torch.float64)
y_mat = np.array(
[[0, 0, 1],
[0, 1, 0]]
)
y_mat = torch.tensor(y_mat, dtype = torch.float32)
y_mat
tensor([[0., 0., 1.],
[0., 1., 0.]])
y_hat_mat = np.array(
[[0.2, 0.2, 0.6],
[0.1, 0.8, 0.1]]
)
y_hat_mat = torch.tensor(y_hat_mat)
y_hat_mat = torch.log(y_hat_mat/(1-y_hat_mat))
y_hat_mat
tensor([[-1.3863, -1.3863, 0.4055],
[-2.1972, 1.3863, -2.1972]], dtype=torch.float64)
from torch import nn
official_loss = nn.CrossEntropyLoss(reduction='none')
official_loss(y_hat_logit_mat, y_mat)
tensor([2.5806, 6.0025], dtype=torch.float64)
official_loss(y_hat_mat, y_vec)
tensor([0.8504, 0.6897], dtype=torch.float64)
class MySparseCategoricalCrossEntropy:
def __init__(self, reduction = "mean"):
self.reduction = reduction
def __call__(self, y_hat_mat, y_vec):
"""
args:
- y_hat_mat: shape = (batch_size, c), c = one_hot_vector_size
- y_vec: shape = (batch_size,), 每個 element 是 int,值介於 0~ (c-1)
"""
loss = -1*torch.log(y_hat_mat[range(len(y_hat_mat)), y_vec])
if self.reduction == "mean":
cost = loss.mean()
if self.reduction == "sum":
cost = loss.sum()
if self.reduction == "none":
cost = loss
return cost
# instance
loss = MySparseCategoricalCrossEntropy(reduction = "none")
y_hat_mat = np.array(
[[0.2, 0.2, 0.6],
[0.1, 0.8, 0.1]]
)
y_hat_mat = torch.tensor(y_hat_mat)
y_vec = np.array([2, 1])
y_vec = torch.tensor(y_vec)
loss(y_hat_mat, y_vec)
tensor([0.5108, 0.2231], dtype=torch.float64)
12.3.3. optimizer¶
一樣用 sgd 就好:
class MySGD:
def __init__(self, params, lr = 0.03):
self.params = params
self.lr = lr
def step(self):
with torch.no_grad():
for param in self.params:
param -= self.lr * param.grad
def zero_grad(self):
for param in self.params:
if param.grad is not None:
param.grad.zero_() # 清空 gradient
# def optimizer(params, lr = 0.03): #@save
# """ sgd """
# with torch.no_grad():
# for param in params:
# param -= lr * param.grad
# param.grad.zero_() # 清空 gradient
12.3.4. metric¶
class MyAcc:
def __init__(self, threshold=0.5, **kwargs):
self.threshold = 0.5
self.true_decision = 0.0
self.total_number = 0.0
def update_state(self, y_hat, y):
# 計算預測正確的數量
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis = 1)
cmp = y_hat.type(y.dtype) == y
self.true_decision += float(cmp.type(y.dtype).sum())
self.total_number += len(y)
def result(self):
if self.total_number == 0:
accuracy = 0.0
else:
accuracy = self.true_decision / self.total_number
return accuracy
def reset_state(self):
self.true_decision = 0.0
self.total_number = 0.0
my_acc = MyAcc()
y_hat = torch.tensor([[0.2, 0.6, 0.2],[0.1,0.1,0.8],[0.9,0.05,0.05]], requires_grad = False)
y = torch.tensor([0, 2, 0], requires_grad = False)
my_acc.update_state(y_hat, y)
my_acc.result()
0.6666666666666666
my_acc.update_state(y_hat, y)
my_acc.result()
0.6666666666666666
my_acc.reset_state()
my_acc.result()
0.0
12.3.5. training¶
這次,來定義一些好用的 function 吧:
def train_epoch(model, train_iter, loss, optimizer, metric):
metric.reset_state()
cost_list = []
for batch, (X, y) in enumerate(train_iter):
# forward
if isinstance(model, torch.nn.Module):
model.train()
y_hat = model(X)
else:
y_hat = model(X, params)
batch_cost = loss(y_hat, y)
metric.update_state(y_hat, y)
# 清空 gradient
optimizer.zero_grad()
# backward
batch_cost.backward() # 算 gradient
optimizer.step() # 更新參數
# add to cost_list
cost_list.append(batch_cost.item())
if batch % 300 == 0:
current_cost = np.array(cost_list).mean()
print(f"batch {batch + 1} training loss: {current_cost}; training accuracy: {metric.result()}")
epoch_cost = np.array(cost_list).mean()
epoch_acc = metric.result()
return epoch_cost, epoch_acc
def valid_epoch(model, test_iter, loss, metric):
metric.reset_state()
if isinstance(model, torch.nn.Module):
model.eval()
with torch.no_grad():
cost_list = []
for X, y in test_iter:
# forward only
if isinstance(model, torch.nn.Module):
y_hat = model(X)
else:
y_hat = model(X, params)
batch_cost = loss(y_hat, y)
cost_list.append(batch_cost.item())
metric.update_state(y_hat, y)
epoch_cost = np.array(cost_list).mean()
epoch_acc = metric.result()
return epoch_cost, epoch_acc
def train(model, train_iter, test_iter, loss, num_epochs, optimizer, metric): #@save
train_history = []
valid_history = []
for epoch in range(num_epochs):
print(f"---------- epoch: {epoch+1} ----------")
train_epoch_cost, train_epoch_acc = train_epoch(model, train_iter, loss, optimizer, metric)
valid_epoch_cost, valid_epoch_acc = valid_epoch(model, test_iter, loss, metric)
print(f"training loss: {train_epoch_cost}; validation loss: {valid_epoch_cost}")
print(f"training acc: {train_epoch_acc}; validation acc: {valid_epoch_acc}")
print("")
train_history.append({"loss": train_epoch_cost, "acc": train_epoch_acc})
valid_history.append({"loss": valid_epoch_cost, "acc": valid_epoch_acc})
return train_history, valid_history
# hyper-parameter
num_epochs = 10
learning_rate = 0.1
# 初始化參數
num_inputs = 28*28
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
params = [W, b]
# loss
loss = MySparseCategoricalCrossEntropy()
# optimizer
optimizer = MySGD(params, lr = learning_rate)
# metric
metric = MyAcc()
# training
train_history, valid_history = train(model, train_iter, test_iter, loss, num_epochs, optimizer, metric)
---------- epoch: 1 ----------
batch 1 training loss: 2.2930948734283447; training accuracy: 0.03125
batch 301 training loss: 0.8190287714978786; training accuracy: 0.7291320598006644
batch 601 training loss: 0.7239517746570702; training accuracy: 0.7584234608985025
batch 901 training loss: 0.6713733558484108; training accuracy: 0.7761861820199778
batch 1201 training loss: 0.6385236556310638; training accuracy: 0.7858295170691091
batch 1501 training loss: 0.6109974273119984; training accuracy: 0.7948034643570953
batch 1801 training loss: 0.5959260584760678; training accuracy: 0.7991220155469184
training loss: 0.5925289306561152; validation loss: 0.5071188468997851
training acc: 0.8003166666666667; validation acc: 0.8237
---------- epoch: 2 ----------
batch 1 training loss: 0.6844662427902222; training accuracy: 0.8125
batch 301 training loss: 0.49228916997925387; training accuracy: 0.8324335548172758
batch 601 training loss: 0.4993857322090279; training accuracy: 0.8273190515806988
batch 901 training loss: 0.49838475749045447; training accuracy: 0.8273446170921198
batch 1201 training loss: 0.49313573891624224; training accuracy: 0.8298293089092423
batch 1501 training loss: 0.4880894674391527; training accuracy: 0.8320078281145903
batch 1801 training loss: 0.4860999575882803; training accuracy: 0.8324368406440866
training loss: 0.48404501222372054; validation loss: 0.4993036704512831
training acc: 0.8329166666666666; validation acc: 0.8322
---------- epoch: 3 ----------
batch 1 training loss: 0.49877896904945374; training accuracy: 0.8125
batch 301 training loss: 0.4654339632619655; training accuracy: 0.8416735880398671
batch 601 training loss: 0.46685775229319953; training accuracy: 0.841514143094842
batch 901 training loss: 0.4642828342222612; training accuracy: 0.8418770810210877
batch 1201 training loss: 0.4630293133331278; training accuracy: 0.8420847210657785
batch 1501 training loss: 0.46148545784921663; training accuracy: 0.842542471685543
batch 1801 training loss: 0.45975072789463584; training accuracy: 0.8423965852304275
training loss: 0.4618278339385986; validation loss: 0.4724312952151314
training acc: 0.8415166666666667; validation acc: 0.8377
---------- epoch: 4 ----------
batch 1 training loss: 0.752126932144165; training accuracy: 0.75
batch 301 training loss: 0.4566462513220271; training accuracy: 0.8402200996677741
batch 601 training loss: 0.45347931152968957; training accuracy: 0.8428660565723793
batch 901 training loss: 0.4574048738021168; training accuracy: 0.8426748057713651
batch 1201 training loss: 0.4538820588916267; training accuracy: 0.8438540799333888
batch 1501 training loss: 0.451838077037911; training accuracy: 0.8448742504996669
batch 1801 training loss: 0.45143803642201197; training accuracy: 0.8444267073847862
training loss: 0.4506406066338221; validation loss: 0.4746488459860555
training acc: 0.8448833333333333; validation acc: 0.8329
---------- epoch: 5 ----------
batch 1 training loss: 0.3627922534942627; training accuracy: 0.84375
batch 301 training loss: 0.44672198222325094; training accuracy: 0.8476951827242525
batch 601 training loss: 0.44790385678385736; training accuracy: 0.8466098169717138
batch 901 training loss: 0.4498924219217999; training accuracy: 0.8464553274139844
batch 1201 training loss: 0.4476724240950601; training accuracy: 0.8468203580349709
batch 1501 training loss: 0.44572621827162084; training accuracy: 0.8484551965356429
batch 1801 training loss: 0.44528925549166526; training accuracy: 0.8479317046085508
training loss: 0.4448719442089399; validation loss: 0.4765161728135313
training acc: 0.8481833333333333; validation acc: 0.8305
---------- epoch: 6 ----------
batch 1 training loss: 0.26377439498901367; training accuracy: 0.90625
batch 301 training loss: 0.438816733633561; training accuracy: 0.8480066445182725
batch 601 training loss: 0.4382005668122836; training accuracy: 0.848481697171381
batch 901 training loss: 0.43852038368930035; training accuracy: 0.8477039400665927
batch 1201 training loss: 0.43726639850972393; training accuracy: 0.8486417568692756
batch 1501 training loss: 0.43858158362559047; training accuracy: 0.8482261825449701
batch 1801 training loss: 0.4411187084771275; training accuracy: 0.8481052193225985
training loss: 0.4408056870738665; validation loss: 0.47684303087929186
training acc: 0.84795; validation acc: 0.8299
---------- epoch: 7 ----------
batch 1 training loss: 0.6044304370880127; training accuracy: 0.75
batch 301 training loss: 0.4405321858055964; training accuracy: 0.8491486710963455
batch 601 training loss: 0.43504094135344723; training accuracy: 0.8507175540765392
batch 901 training loss: 0.4337968794209314; training accuracy: 0.8504786348501665
batch 1201 training loss: 0.4375404339596989; training accuracy: 0.8488499167360533
batch 1501 training loss: 0.43609161344887337; training accuracy: 0.8500999333777481
batch 1801 training loss: 0.4356451380267731; training accuracy: 0.8500832870627429
training loss: 0.4355355701724688; validation loss: 0.4765955810063182
training acc: 0.8500833333333333; validation acc: 0.8313
---------- epoch: 8 ----------
batch 1 training loss: 0.5011204481124878; training accuracy: 0.8125
batch 301 training loss: 0.44911604077614026; training accuracy: 0.8490448504983389
batch 601 training loss: 0.4359223718279213; training accuracy: 0.8520694675540765
batch 901 training loss: 0.42745239596057283; training accuracy: 0.8539816870144284
batch 1201 training loss: 0.4263410305388762; training accuracy: 0.8536896336386345
batch 1501 training loss: 0.4269639897612553; training accuracy: 0.8531812125249834
batch 1801 training loss: 0.4291854333473801; training accuracy: 0.8523736812881733
training loss: 0.4298478712320328; validation loss: 0.46099243877223506
training acc: 0.8521333333333333; validation acc: 0.8414
---------- epoch: 9 ----------
batch 1 training loss: 0.3525997996330261; training accuracy: 0.9375
batch 301 training loss: 0.4286440979701736; training accuracy: 0.8513289036544851
batch 601 training loss: 0.43236852765777545; training accuracy: 0.8509255407653911
batch 901 training loss: 0.4297431426889756; training accuracy: 0.8513110432852387
batch 1201 training loss: 0.43217974043234897; training accuracy: 0.8498386761032473
batch 1501 training loss: 0.43002170976065224; training accuracy: 0.8499125582944703
batch 1801 training loss: 0.431127583298797; training accuracy: 0.8499791782343142
training loss: 0.4303571875214577; validation loss: 0.47739782224828825
training acc: 0.8500333333333333; validation acc: 0.8355
---------- epoch: 10 ----------
batch 1 training loss: 0.4089989960193634; training accuracy: 0.8125
batch 301 training loss: 0.4038677517064782; training accuracy: 0.8604651162790697
batch 601 training loss: 0.42295997381557443; training accuracy: 0.8531094009983361
batch 901 training loss: 0.4204221637578439; training accuracy: 0.8530452275249722
batch 1201 training loss: 0.4241272190230574; training accuracy: 0.8523886344712739
batch 1501 training loss: 0.4252326993853707; training accuracy: 0.8515572951365756
batch 1801 training loss: 0.42654917436728934; training accuracy: 0.8516796224319823
training loss: 0.426084530989329; validation loss: 0.47719197420361703
training acc: 0.8522; validation acc: 0.8313
12.3.6. prediction¶
现在训练已经完成,我们的模型已经准备好[对图像进行分类预测]。 给定一系列图像,我们将比较它们的实际标签(文本输出的第一行)和模型预测(文本输出的第二行)。
def my_predict(model, test_iter, n=6): #@save
"""预测标签(定义见第3章)"""
for X, y in test_iter:
break # 只取第一個 batch 的意思
print(y)
trues = get_fashion_mnist_labels(y)
preds = get_fashion_mnist_labels(model(X, params).argmax(axis=1))
titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
show_images(
X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
my_predict(model, test_iter)
tensor([9, 2, 1, 1, 6, 1, 4, 6, 5, 7, 4, 5, 7, 3, 4, 1, 2, 4, 8, 0, 2, 5, 7, 9,
1, 4, 6, 0, 9, 3, 8, 8])
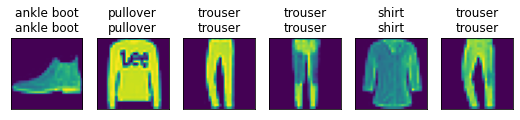
12.4. 內建 function¶
12.4.1. 定義模型¶
from torch import nn
model = nn.Sequential(
nn.Flatten(),
nn.Linear(28*28, 10)
)
12.4.2. loss function¶
用內建的
nn.CrossEntropyLoss(),使用方法和之前一樣:loss = nn.CrossEntropyLoss(),然後loss(y_hat, y)要注意的是:
y_hat 要放的是 logits (還沒做 softmax)的結果。這樣做的原因,是因為數值的穩定性的考量.
y 可以放 [0, C) 的 integer,或是 one-hot encoding (但 dtype 要改為 float32,原因是可以通用到 blended-label).
loss = nn.CrossEntropyLoss(reduction='mean')
12.4.3. optimizer¶
optimizer = torch.optim.SGD(model.parameters(), lr = 0.1)
12.4.4. metric¶
metric = MyAcc()
12.4.5. training¶
train_history, valid_history = train(model, train_iter, test_iter, loss, num_epochs, optimizer, metric)
---------- epoch: 1 ----------
batch 1 training loss: 0.2760540843009949; training accuracy: 0.90625
batch 301 training loss: 0.4194850102562049; training accuracy: 0.8523671096345515
batch 601 training loss: 0.4186703875884042; training accuracy: 0.8544093178036606
batch 901 training loss: 0.4168739371936144; training accuracy: 0.853808268590455
batch 1201 training loss: 0.41391293170375687; training accuracy: 0.8543921731890092
batch 1501 training loss: 0.4162772057961417; training accuracy: 0.8542638241172552
batch 1801 training loss: 0.41838816321273437; training accuracy: 0.8537791504719601
training loss: 0.42017893958886465; validation loss: 0.4601927140412239
training acc: 0.8530666666666666; validation acc: 0.8414
---------- epoch: 2 ----------
batch 1 training loss: 0.39312267303466797; training accuracy: 0.8125
batch 301 training loss: 0.407473469914194; training accuracy: 0.8565199335548173
batch 601 training loss: 0.40750258228743136; training accuracy: 0.8571651414309485
batch 901 training loss: 0.4134164113183397; training accuracy: 0.8550221975582686
batch 1201 training loss: 0.4172303157980297; training accuracy: 0.8538197335553706
batch 1501 training loss: 0.41699684872915554; training accuracy: 0.8539931712191872
batch 1801 training loss: 0.4182056664907555; training accuracy: 0.8538312048861744
training loss: 0.4167207231005033; validation loss: 0.4617531546198141
training acc: 0.8543666666666667; validation acc: 0.8386
---------- epoch: 3 ----------
batch 1 training loss: 0.21020445227622986; training accuracy: 0.9375
batch 301 training loss: 0.39938764736996935; training accuracy: 0.8596345514950167
batch 601 training loss: 0.40986907363136277; training accuracy: 0.8578410981697171
batch 901 training loss: 0.4162394596257564; training accuracy: 0.8558892896781354
batch 1201 training loss: 0.41704956571153556; training accuracy: 0.8555890924229809
batch 1501 training loss: 0.42006259712872707; training accuracy: 0.8543471019320453
batch 1801 training loss: 0.4183133905055389; training accuracy: 0.8545773181565797
training loss: 0.4184689321398735; validation loss: 0.47002472833227427
training acc: 0.8545166666666667; validation acc: 0.8372
---------- epoch: 4 ----------
batch 1 training loss: 0.5089763402938843; training accuracy: 0.8125
batch 301 training loss: 0.4168938092664627; training accuracy: 0.8573504983388704
batch 601 training loss: 0.4145228750693818; training accuracy: 0.8572691347753744
batch 901 training loss: 0.4180211562841105; training accuracy: 0.8556811875693674
batch 1201 training loss: 0.41757332773058736; training accuracy: 0.8550947127393839
batch 1501 training loss: 0.41422225450035893; training accuracy: 0.8566788807461693
batch 1801 training loss: 0.4140817682852949; training accuracy: 0.8573188506385342
training loss: 0.41417200604279836; validation loss: 0.5011046351954198
training acc: 0.8572833333333333; validation acc: 0.8279
---------- epoch: 5 ----------
batch 1 training loss: 0.37356817722320557; training accuracy: 0.875
batch 301 training loss: 0.4041610992578573; training accuracy: 0.8588039867109635
batch 601 training loss: 0.4117486807897365; training accuracy: 0.8563331946755408
batch 901 training loss: 0.4119780889064173; training accuracy: 0.8567216981132075
batch 1201 training loss: 0.4130154121713674; training accuracy: 0.8561875520399667
batch 1501 training loss: 0.4119384880118732; training accuracy: 0.8564915056628915
batch 1801 training loss: 0.4138048914556434; training accuracy: 0.8566247917823432
training loss: 0.413866045721372; validation loss: 0.4563162605316875
training acc: 0.85675; validation acc: 0.8408
---------- epoch: 6 ----------
batch 1 training loss: 0.3489759862422943; training accuracy: 0.84375
batch 301 training loss: 0.4100171427344563; training accuracy: 0.8557931893687708
batch 601 training loss: 0.4145066224274143; training accuracy: 0.8543053244592346
batch 901 training loss: 0.41525910867504223; training accuracy: 0.853912319644839
batch 1201 training loss: 0.41507272571821596; training accuracy: 0.8541840133222315
batch 1501 training loss: 0.4156796067039781; training accuracy: 0.854721852098601
batch 1801 training loss: 0.41509056804926114; training accuracy: 0.855479594669628
training loss: 0.4149472252488136; validation loss: 0.4544931400698214
training acc: 0.8554833333333334; validation acc: 0.8421
---------- epoch: 7 ----------
batch 1 training loss: 0.3232419490814209; training accuracy: 0.90625
batch 301 training loss: 0.399986172806583; training accuracy: 0.8583887043189369
batch 601 training loss: 0.4029200790874573; training accuracy: 0.8593490016638935
batch 901 training loss: 0.40746594569361566; training accuracy: 0.8582824639289678
batch 1201 training loss: 0.41075665754988033; training accuracy: 0.856473771856786
batch 1501 training loss: 0.41316802269077396; training accuracy: 0.8555129913391073
batch 1801 training loss: 0.4123198016071439; training accuracy: 0.8559827873403665
training loss: 0.4123239260236422; validation loss: 0.5108196877728636
training acc: 0.8556166666666667; validation acc: 0.8259
---------- epoch: 8 ----------
batch 1 training loss: 0.2686026692390442; training accuracy: 0.90625
batch 301 training loss: 0.39633925354411437; training accuracy: 0.8620224252491694
batch 601 training loss: 0.4100435714170758; training accuracy: 0.8579970881863561
batch 901 training loss: 0.40710506402576274; training accuracy: 0.8581090455049944
batch 1201 training loss: 0.405784776792563; training accuracy: 0.8581650707743547
batch 1501 training loss: 0.4074982617678323; training accuracy: 0.8576782145236509
batch 1801 training loss: 0.4099115320749742; training accuracy: 0.8569544697390339
training loss: 0.40996687454183894; validation loss: 0.5048220109063596
training acc: 0.85685; validation acc: 0.8333
---------- epoch: 9 ----------
batch 1 training loss: 0.5238355398178101; training accuracy: 0.75
batch 301 training loss: 0.3980180616691659; training accuracy: 0.8650332225913622
batch 601 training loss: 0.40896938309792474; training accuracy: 0.8596089850249584
batch 901 training loss: 0.4058504473670209; training accuracy: 0.8582477802441731
batch 1201 training loss: 0.40951391710255364; training accuracy: 0.8576446711074105
batch 1501 training loss: 0.4083509028484073; training accuracy: 0.8581362425049966
batch 1801 training loss: 0.4099285071017608; training accuracy: 0.8576832315380344
training loss: 0.41094837238788606; validation loss: 0.4975788382866893
training acc: 0.85745; validation acc: 0.8218
---------- epoch: 10 ----------
batch 1 training loss: 0.4953480064868927; training accuracy: 0.75
batch 301 training loss: 0.39248133037375454; training accuracy: 0.863891196013289
batch 601 training loss: 0.40346336842029545; training accuracy: 0.8597649750415973
batch 901 training loss: 0.40110374794452225; training accuracy: 0.8599125971143174
batch 1201 training loss: 0.4051802050288174; training accuracy: 0.8586074104912573
batch 1501 training loss: 0.4077464541659841; training accuracy: 0.8582611592271818
batch 1801 training loss: 0.4072158080688587; training accuracy: 0.858411993337035
training loss: 0.4082008256157239; validation loss: 0.46867902812580714
training acc: 0.8582833333333333; validation acc: 0.8386
12.5. 內建 VS 自己寫的差別¶
主要在 loss function,內建的
nn.CrossEntropyLoss()放進去的 y_hat 必須是 logits,不能是 softmax 後的機率值。所以,在定義模型時,內建的 model,必須將輸定為 logit (i.e. 只用 linear 層,沒有用 nn.softmax() 層),但自己 from scratch 建的時候,model 的輸出是要經過 softmax 的處理
至於,為啥內建
nn.CrossEntropyLoss()一定要餵 logits 給他,是因為數值穩定性的考量d2l 的
3.7 Softmax回歸的簡潔實現有很清楚的說明,再去看就好,有空再整理過來。
