Histograms and Density
Contents
9. Histograms and Density¶
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
9.1. 一維的直方圖¶
一個簡單的直方圖,就用
plt.hist()就可以完成:
data = np.random.randn(1000)
plt.hist(data);
我們還有很多客製化的參數可以下:
plt.hist(data,
bins=30,
color='steelblue',
edgecolor='none',
histtype='stepfilled',
alpha=0.5);
如果想得到分類後的數據就好,那可以這樣做
counts, bin_edges = np.histogram(data, bins=5)
print(bin_edges) # 每個bin的起點終點
print(counts) # 每個 bin 對應到的次數
[-3.09793211 -1.77395464 -0.44997717 0.87400031 2.19797778 3.52195525]
[ 43 279 480 181 17]
如果要同時畫多個 histogram,那就多做幾次
plt.hist()就好:
x1 = np.random.normal(0, 0.8, 1000)
x2 = np.random.normal(-2, 1, 1000)
x3 = np.random.normal(3, 2, 1000)
kwargs = dict(histtype='stepfilled', alpha=0.3, bins=40)
plt.hist(x1, **kwargs)
plt.hist(x2, **kwargs)
plt.hist(x3, **kwargs);
9.2. 二維的直方圖¶
# 生出二維常態的資料
mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T
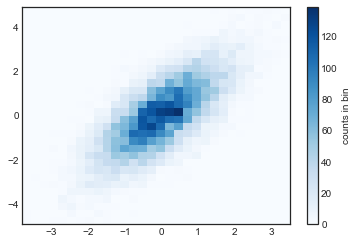
9.2.1. plt.hist2d: 二維直方圖¶
剛剛一維的 histogram,是用
plt.hist()來畫,現在二維的 histogram,是用plt.hist2d()來畫.
plt.hist2d(x, y, bins=30, cmap='Blues')
cb = plt.colorbar()
cb.set_label('counts in bin')
就像剛剛可以用
np.histogram()來得到組別和各組的count的訊息,現在可以用np.histogram2d()來得到各組的組別(就是x和y的range)以及組別的count。作法如下:
counts, xedges, yedges = np.histogram2d(x, y, bins=30)
print(counts)
print(xedges)
print(yedges)
[[ 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 1. 0. 0. 0. 0. 2. 0. 1. 1. 0. 2. 0. 1. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 1. 0. 4. 7. 1. 1. 3. 3. 1. 0. 0. 0. 1. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 3. 6. 3. 7. 4. 3. 5. 3. 4. 5. 2. 1. 0.
1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 1. 0. 2. 1. 6. 10. 8. 9. 8. 10. 10. 9. 3. 2.
1. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 2. 0. 3. 3. 7. 17. 9. 18. 14. 24. 14. 13. 10. 8.
0. 1. 2. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 3. 1. 3. 9. 15. 15. 24. 25. 33. 21. 28. 19. 16.
10. 6. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 1. 1. 1. 5. 6. 14. 20. 22. 35. 34. 42. 42. 43. 28.
12. 7. 2. 4. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 1. 0. 3. 10. 21. 31. 36. 53. 59. 58. 50. 57.
34. 32. 16. 5. 4. 2. 1. 1. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 2. 11. 9. 22. 43. 49. 75. 60. 70. 63.
59. 33. 22. 22. 12. 1. 1. 3. 0. 1. 0. 0. 0. 0.
0. 0.]
[ 0. 1. 0. 2. 1. 5. 13. 23. 28. 57. 69. 91. 108. 83.
77. 53. 48. 32. 21. 10. 4. 2. 0. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 1. 7. 9. 17. 40. 44. 68. 97. 105. 118.
119. 111. 70. 38. 22. 12. 6. 4. 2. 1. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 1. 4. 13. 26. 43. 50. 78. 108. 127.
107. 119. 115. 65. 60. 39. 14. 7. 4. 0. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 1. 0. 2. 18. 27. 56. 66. 91. 107.
117. 130. 113. 89. 76. 36. 32. 18. 6. 2. 0. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 1. 1. 1. 9. 15. 31. 53. 76. 63.
106. 133. 119. 82. 90. 68. 40. 26. 10. 5. 2. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 2. 7. 5. 17. 29. 32. 77.
103. 139. 107. 106. 101. 56. 51. 28. 14. 7. 4. 0. 0. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 2. 1. 0. 5. 9. 12. 28. 35.
73. 71. 95. 88. 80. 72. 69. 41. 22. 13. 5. 4. 0. 1.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 8. 4. 7. 18. 27.
37. 57. 69. 73. 73. 63. 52. 43. 40. 11. 5. 5. 1. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 8. 9. 8.
22. 37. 41. 57. 54. 61. 45. 37. 27. 24. 9. 6. 1. 0.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2. 5. 8.
13. 24. 22. 40. 51. 37. 39. 30. 25. 24. 15. 10. 1. 0.
0. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2. 3.
10. 14. 13. 15. 30. 23. 39. 22. 21. 11. 11. 6. 6. 1.
0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 3.
1. 2. 4. 8. 18. 22. 21. 26. 14. 19. 10. 4. 3. 3.
2. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.
1. 0. 1. 3. 8. 9. 13. 13. 8. 7. 14. 5. 5. 0.
3. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
1. 1. 1. 3. 3. 4. 5. 12. 7. 7. 6. 5. 2. 1.
0. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 2. 0. 5. 1. 3. 3. 3. 2. 4. 2.
2. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 1. 2. 2. 3. 1. 1. 1. 0.
1. 2.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 1. 2. 1. 2. 0. 3.
0. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 1. 0. 0.
2. 0.]]
[-3.80099282 -3.55740187 -3.31381093 -3.07021999 -2.82662904 -2.5830381
-2.33944716 -2.09585621 -1.85226527 -1.60867433 -1.36508338 -1.12149244
-0.8779015 -0.63431055 -0.39071961 -0.14712867 0.09646228 0.34005322
0.58364416 0.82723511 1.07082605 1.31441699 1.55800794 1.80159888
2.04518982 2.28878077 2.53237171 2.77596265 3.0195536 3.26314454
3.50673548]
[-4.91027112e+00 -4.58299194e+00 -4.25571276e+00 -3.92843359e+00
-3.60115441e+00 -3.27387523e+00 -2.94659606e+00 -2.61931688e+00
-2.29203770e+00 -1.96475853e+00 -1.63747935e+00 -1.31020017e+00
-9.82920995e-01 -6.55641818e-01 -3.28362641e-01 -1.08346439e-03
3.26195713e-01 6.53474889e-01 9.80754066e-01 1.30803324e+00
1.63531242e+00 1.96259160e+00 2.28987077e+00 2.61714995e+00
2.94442913e+00 3.27170830e+00 3.59898748e+00 3.92626666e+00
4.25354584e+00 4.58082501e+00 4.90810419e+00]
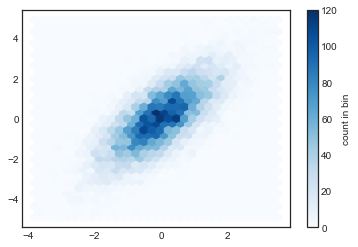
plt.hexbin(x, y, gridsize=30, cmap='Blues')
cb = plt.colorbar(label='count in bin')
9.2.2. Kernel density estimation¶
我們也可以去估計二維分配的 density,例如,我假設資料服從二維常態,然後去估計他
我們可以用
scipy.stats這個 module
from scipy.stats import gaussian_kde
# fit an array of size [Ndim, Nsamples]
data = np.vstack([x, y])
kde = gaussian_kde(data)
# evaluate on a regular grid
xgrid = np.linspace(-3.5, 3.5, 40)
ygrid = np.linspace(-6, 6, 40)
Xgrid, Ygrid = np.meshgrid(xgrid, ygrid)
Z = kde.evaluate(np.vstack([Xgrid.ravel(), Ygrid.ravel()]))
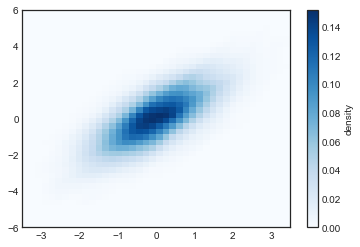
# Plot the result as an image
plt.imshow(Z.reshape(Xgrid.shape),
origin='lower', aspect='auto',
extent=[-3.5, 3.5, -6, 6],
cmap='Blues')
cb = plt.colorbar()
cb.set_label("density")
之後在 深入研究: 核密度估計的章節,會介紹 kernel density的估計方法。
後面的 使用seaborn進行視覺化,也會介紹seaborn更簡潔的語法,做到更客製化的繪圖。
