20. Permutation Importance vs Random Forest Feature Importance (MDI)¶

在這個範例中，我們要比較以下這兩種方法，在 titanic dataset 這個分類問題中的變數重要性結果：
- sklearn.ensemble.RandomForestClassifier 的 impurity-based feature importance
- sklearn.inspection.permutation_importance 的 permutation importance
我們將展示，impurity-based feature importance 有可能誇大了 numerical feature 的重要性.
先講結論：
- 做 rf 或 tree-based model時，我們必須把 categorical variable 先做 onehot，所以最後算 impurity-based importance 的時候，同一個類別變數被稀釋掉了.
- 另一個 impurity-based importance 的潛在問題是(看不太懂)： the impurity-based feature importance of random forests suffers from being computed on statistics derived from the training dataset: the importances can be high even for features that are not predictive of the target variable, as long as the model has the capacity to use them to overfit.
- 所以，如果你的變數有類別有連續，建議用 permutation-based importance

import matplotlib.pyplot as plt
import numpy as np

# data 區
from sklearn.datasets import fetch_openml

# 前處理
from sklearn.preprocessing import OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer

# 分割資料
from sklearn.model_selection import train_test_split

# model
from sklearn.ensemble import RandomForestClassifier

# importance
from sklearn.inspection import permutation_importance

20.1. Data Loading and Feature Engineering¶

我們先 load 資料集

X, y = fetch_openml("titanic", version=1, as_frame=True, return_X_y=True)
X.head()

	pclass	name	sex	age	sibsp	parch	ticket	fare	cabin	embarked	boat	body	home.dest
0	1.0	Allen, Miss. Elisabeth Walton	female	29.0000	0.0	0.0	24160	211.3375	B5	S	2	NaN	St Louis, MO
1	1.0	Allison, Master. Hudson Trevor	male	0.9167	1.0	2.0	113781	151.5500	C22 C26	S	11	NaN	Montreal, PQ / Chesterville, ON
2	1.0	Allison, Miss. Helen Loraine	female	2.0000	1.0	2.0	113781	151.5500	C22 C26	S	None	NaN	Montreal, PQ / Chesterville, ON
3	1.0	Allison, Mr. Hudson Joshua Creighton	male	30.0000	1.0	2.0	113781	151.5500	C22 C26	S	None	135.0	Montreal, PQ / Chesterville, ON
4	1.0	Allison, Mrs. Hudson J C (Bessie Waldo Daniels)	female	25.0000	1.0	2.0	113781	151.5500	C22 C26	S	None	NaN	Montreal, PQ / Chesterville, ON

然後，我們新增兩個 column，一個連續型，一個類別型，他們都和我的 y 無關
- random_num is a high cardinality numerical variable (as many unique values as records).
- random_cat is a low cardinality categorical variable (3 possible values).

rng = np.random.RandomState(seed=42)
X["random_cat"] = rng.randint(3, size=X.shape[0])
X["random_num"] = rng.randn(X.shape[0])

X.random_cat.head()

  2
  0
  2
  2
  0
Name: random_cat, dtype: int64

接下來，就來 fit model 吧：

categorical_columns = ["pclass", "sex", "embarked", "random_cat"]
numerical_columns = ["age", "sibsp", "parch", "fare", "random_num"]

X = X[categorical_columns + numerical_columns]

# 分割資料
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

# 前處理
categorical_encoder = OneHotEncoder(handle_unknown="ignore")
numerical_pipe = Pipeline([("imputer", SimpleImputer(strategy="mean"))])

preprocessing = ColumnTransformer(
    [
        ("cat", categorical_encoder, categorical_columns),
        ("num", numerical_pipe, numerical_columns),
    ]
)

rf = Pipeline(
    [
        ("preprocess", preprocessing),
        ("classifier", RandomForestClassifier(random_state=42)),
    ]
)

# fit model
rf.fit(X_train, y_train)

Pipeline(steps=[('preprocess',
                 ColumnTransformer(transformers=[('cat',
                                                  OneHotEncoder(handle_unknown='ignore'),
                                                  ['pclass', 'sex', 'embarked',
                                                   'random_cat']),
                                                 ('num',
                                                  Pipeline(steps=[('imputer',
                                                                   SimpleImputer())]),
                                                  ['age', 'sibsp', 'parch',
                                                   'fare', 'random_num'])])),
                ('classifier', RandomForestClassifier(random_state=42))])

20.2. Accuracy of the Model¶

在檢查變數重要性前，我們要先確認 model 夠準了。因為如果不準的話，我們對於變數重要性的探索是沒啥興趣的。

print(f"RF train accuracy: {rf.score(X_train, y_train)}")
print(f"RF test accuracy: {rf.score(X_test, y_test)}") 

RF train accuracy: 1.0
RF test accuracy: 0.8170731707317073

可以看到 training set 超猛的，但也不算 overfitting 太嚴重，因為 testing set 還有 0.81
所以，還有可能去 tune hyper-parameter，來讓 training set 爛一點，然後 testing set 好一點，例如：min_samples_leaf 設大一點(e.g. 從 =5 變成 =10)，讓最終的節點數量多一些，避免overfitting)
但沒差，這不是今天的重點，我們現在就假裝這個 model 夠好了，來看看 feature importance 的議題吧

20.3. Tree’s Feature Importance from Mean Decrease in Impurity (MDI)¶

ohe = rf.named_steps["preprocess"].named_transformers_["cat"] # 取出 one-hot encoding 的 transformer
feature_names = ohe.get_feature_names_out(categorical_columns) # 取出類別變數(categorical_columns)做完one-hot後的名稱
feature_names = np.r_[feature_names, numerical_columns] # 最終的變數就是這些 [類別s, 連續s]

tree_feature_importances = rf.named_steps["classifier"].feature_importances_ # 結果是 [0.025, 0.01, ..., 0.18] 這種 list，裡面都是mean decrease in impurity(i.e. gini)
sorted_idx = tree_feature_importances.argsort() # 得到 [6,1,...,15]，就是排名吧

y_ticks = np.arange(0, len(feature_names))
fig, ax = plt.subplots()
ax.barh(y_ticks, tree_feature_importances[sorted_idx])
ax.set_yticks(y_ticks)
ax.set_yticklabels(feature_names[sorted_idx])
ax.set_title("Random Forest Feature Importances (MDI)")
fig.tight_layout()
plt.show()

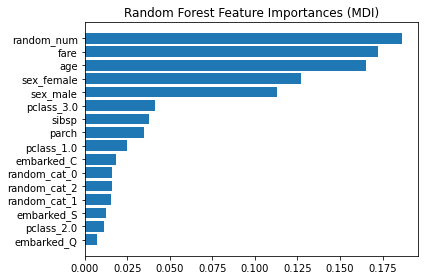
結果顯示，最重要的 feature 是 numerical features 中的 random_num…傻眼！！
會有這樣的問題，是因為 impurity-based featrue importances 的兩個限制：
- impurity-based importances are biased towards high cardinality features; (一個集合的cardinality，就是該集合的unique元素的個數)
- impurity-based importances are computed on training set statistics and therefore do not reflect the ability of feature to be useful to make predictions that generalize to the test set (when the model has enough capacity).
但另一方面，如果用 permutation importances，他是用 test set 來計算重要性的，他的結果就天差地別：

result = permutation_importance(
    rf, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
sorted_idx = result.importances_mean.argsort()

fig, ax = plt.subplots()
ax.boxplot(
    result.importances[sorted_idx].T, vert=False, labels=X_test.columns[sorted_idx]
)
ax.set_title("Permutation Importances (test set)")
fig.tight_layout()
plt.show()

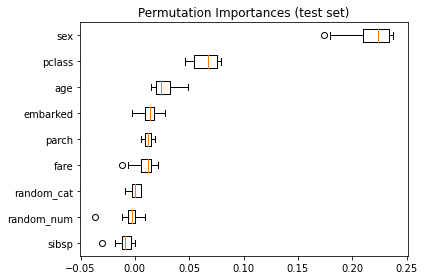
可以看到，如預期的，random_num 的重要性降的極低.
如果，你用 training set 來計算 permutation，結果會變成

result = permutation_importance(
    rf, X_train, y_train, n_repeats=10, random_state=42, n_jobs=2
)
sorted_idx = result.importances_mean.argsort()

fig, ax = plt.subplots()
ax.boxplot(
    result.importances[sorted_idx].T, vert=False, labels=X_train.columns[sorted_idx]
)
ax.set_title("Permutation Importances (train set)")
fig.tight_layout()
plt.show()

可以看到， random_num 在 training set 的重要性明顯比在 testing set 的重要性高.
這兩張圖的對比，可以了解到 rf model 大概是用了 random_num 來 overfit data 了。
你可以重 run 這個 example，但把 RF 的超參數 min_samples_leaf 改設為 10，就可以發現當 training set 沒有 overfitting 時，你用 training set 或 testing set 做 permutation test，節果是差不多的。

My sample book

Permutation Importance vs Random Forest Feature Importance (MDI)

Contents

20. Permutation Importance vs Random Forest Feature Importance (MDI)¶

20.1. Data Loading and Feature Engineering¶

20.2. Accuracy of the Model¶

20.3. Tree’s Feature Importance from Mean Decrease in Impurity (MDI)¶