14. Clustering¶

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris

14.1. K-Means¶

14.1.1. toy-example (iris)¶

出動 iris 資料集吧

iris = load_iris()
df_data = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
                     columns= ['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species'])
df_data

	SepalLengthCm	SepalWidthCm	PetalLengthCm	PetalWidthCm	Species
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

150 rows × 5 columns

from sklearn.cluster import KMeans


X = df_data.drop("Species", axis = 1)
kmeansModel = KMeans(n_clusters=3, # 分 3 群
                     n_init = 10, # 起始值有10組，每組分完後，比 inertia，選最小的那組給你
                     random_state=46, # 產出 10 組起始值時，用的 seed
                    tol = 0.0001) # 前後兩次 iteration， centers 間的 歐式距離，小於 0.0001 就算收斂
kmeansModel.fit(X)
clusters_pred = kmeansModel.predict(X)

分群結果

clusters_pred

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
       2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2,
       2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0], dtype=int32)

各群的中心

kmeansModel.cluster_centers_

array([[5.9016129 , 2.7483871 , 4.39354839, 1.43387097],
       [5.006     , 3.428     , 1.462     , 0.246     ],
       [6.85      , 3.07368421, 5.74210526, 2.07105263]])

inertia (within-group sum of variance)

kmeansModel.inertia_

78.85144142614601

選 k

kmeans_list = [KMeans(n_clusters=k, random_state=46).fit(X)
                for k in range(1, 10)]
inertias = [model.inertia_ for model in kmeans_list]

plt.plot(range(1,10), inertias);

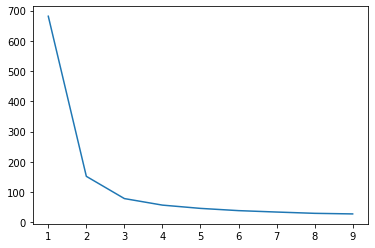
可以看到，elbow 在 2 or 3，所以可以選 2 or 3 當分群的群數

詳細說明文件，看 KMeans?

KMeans?

Init signature:
KMeans(
    n_clusters=8,
    *,
    init='k-means++',
    n_init=10,
    max_iter=300,
    tol=0.0001,
    verbose=0,
    random_state=None,
    copy_x=True,
    algorithm='auto',
)
Docstring:     
K-Means clustering.

Read more in the :ref:`User Guide <k_means>`.

Parameters
----------

n_clusters : int, default=8
    The number of clusters to form as well as the number of
    centroids to generate.

init : {'k-means++', 'random'}, callable or array-like of shape             (n_clusters, n_features), default='k-means++'
    Method for initialization:

    'k-means++' : selects initial cluster centers for k-mean
    clustering in a smart way to speed up convergence. See section
    Notes in k_init for more details.

    'random': choose `n_clusters` observations (rows) at random from data
    for the initial centroids.

    If an array is passed, it should be of shape (n_clusters, n_features)
    and gives the initial centers.

    If a callable is passed, it should take arguments X, n_clusters and a
    random state and return an initialization.

n_init : int, default=10
    Number of time the k-means algorithm will be run with different
    centroid seeds. The final results will be the best output of
    n_init consecutive runs in terms of inertia.

max_iter : int, default=300
    Maximum number of iterations of the k-means algorithm for a
    single run.

tol : float, default=1e-4
    Relative tolerance with regards to Frobenius norm of the difference
    in the cluster centers of two consecutive iterations to declare
    convergence.

verbose : int, default=0
    Verbosity mode.

random_state : int, RandomState instance or None, default=None
    Determines random number generation for centroid initialization. Use
    an int to make the randomness deterministic.
    See :term:`Glossary <random_state>`.

copy_x : bool, default=True
    When pre-computing distances it is more numerically accurate to center
    the data first. If copy_x is True (default), then the original data is
    not modified. If False, the original data is modified, and put back
    before the function returns, but small numerical differences may be
    introduced by subtracting and then adding the data mean. Note that if
    the original data is not C-contiguous, a copy will be made even if
    copy_x is False. If the original data is sparse, but not in CSR format,
    a copy will be made even if copy_x is False.

algorithm : {"auto", "full", "elkan"}, default="auto"
    K-means algorithm to use. The classical EM-style algorithm is "full".
    The "elkan" variation is more efficient on data with well-defined
    clusters, by using the triangle inequality. However it's more memory
    intensive due to the allocation of an extra array of shape
    (n_samples, n_clusters).

    For now "auto" (kept for backward compatibility) chooses "elkan" but it
    might change in the future for a better heuristic.

    .. versionchanged:: 0.18
        Added Elkan algorithm

Attributes
----------
cluster_centers_ : ndarray of shape (n_clusters, n_features)
    Coordinates of cluster centers. If the algorithm stops before fully
    converging (see ``tol`` and ``max_iter``), these will not be
    consistent with ``labels_``.

labels_ : ndarray of shape (n_samples,)
    Labels of each point

inertia_ : float
    Sum of squared distances of samples to their closest cluster center,
    weighted by the sample weights if provided.

n_iter_ : int
    Number of iterations run.

n_features_in_ : int
    Number of features seen during :term:`fit`.

    .. versionadded:: 0.24

feature_names_in_ : ndarray of shape (`n_features_in_`,)
    Names of features seen during :term:`fit`. Defined only when `X`
    has feature names that are all strings.

    .. versionadded:: 1.0

See Also
--------
MiniBatchKMeans : Alternative online implementation that does incremental
    updates of the centers positions using mini-batches.
    For large scale learning (say n_samples > 10k) MiniBatchKMeans is
    probably much faster than the default batch implementation.

Notes
-----
The k-means problem is solved using either Lloyd's or Elkan's algorithm.

The average complexity is given by O(k n T), where n is the number of
samples and T is the number of iteration.

The worst case complexity is given by O(n^(k+2/p)) with
n = n_samples, p = n_features. (D. Arthur and S. Vassilvitskii,
'How slow is the k-means method?' SoCG2006)

In practice, the k-means algorithm is very fast (one of the fastest
clustering algorithms available), but it falls in local minima. That's why
it can be useful to restart it several times.

If the algorithm stops before fully converging (because of ``tol`` or
``max_iter``), ``labels_`` and ``cluster_centers_`` will not be consistent,
i.e. the ``cluster_centers_`` will not be the means of the points in each
cluster. Also, the estimator will reassign ``labels_`` after the last
iteration to make ``labels_`` consistent with ``predict`` on the training
set.

Examples
--------

>>> from sklearn.cluster import KMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
...               [10, 2], [10, 4], [10, 0]])
>>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
>>> kmeans.labels_
array([1, 1, 1, 0, 0, 0], dtype=int32)
>>> kmeans.predict([[0, 0], [12, 3]])
array([1, 0], dtype=int32)
>>> kmeans.cluster_centers_
array([[10.,  2.],
       [ 1.,  2.]])
File:           /Volumes/GoogleDrive/我的雲端硬碟/0. codepool_python/python_ds/python_ds_env/lib/python3.8/site-packages/sklearn/cluster/_kmeans.py
Type:           type
Subclasses:     MiniBatchKMeans

14.1.2. stock movement¶

這個應用蠻好玩的，我們可以對股票的 “走勢” 做分群。
資料如以下：

movements = pd.read_csv("data/company-stock-movements.csv", index_col = 0)
movements.head()

	2010-01-04	2010-01-05	2010-01-06	2010-01-07	2010-01-08	2010-01-11	2010-01-12	2010-01-13	2010-01-14	2010-01-15	...	2013-10-16	2013-10-17	2013-10-18	2013-10-21	2013-10-22	2013-10-23	2013-10-24	2013-10-25	2013-10-28	2013-10-29
Apple	0.580000	-0.220005	-3.409998	-1.170000	1.680011	-2.689994	-1.469994	2.779997	-0.680003	-4.999995	...	0.320008	4.519997	2.899987	9.590019	-6.540016	5.959976	6.910011	-5.359962	0.840019	-19.589981
AIG	-0.640002	-0.650000	-0.210001	-0.420000	0.710001	-0.200001	-1.130001	0.069999	-0.119999	-0.500000	...	0.919998	0.709999	0.119999	-0.480000	0.010002	-0.279998	-0.190003	-0.040001	-0.400002	0.660000
Amazon	-2.350006	1.260009	-2.350006	-2.009995	2.960006	-2.309997	-1.640007	1.209999	-1.790001	-2.039994	...	2.109985	3.699982	9.570008	-3.450013	4.820008	-4.079986	2.579986	4.790009	-1.760009	3.740021
American express	0.109997	0.000000	0.260002	0.720002	0.190003	-0.270001	0.750000	0.300004	0.639999	-0.130001	...	0.680001	2.290001	0.409996	-0.069999	0.100006	0.069999	0.130005	1.849999	0.040001	0.540001
Boeing	0.459999	1.770000	1.549999	2.690003	0.059997	-1.080002	0.360000	0.549999	0.530002	-0.709999	...	1.559997	2.480003	0.019997	-1.220001	0.480003	3.020004	-0.029999	1.940002	1.130005	0.309998

5 rows × 963 columns

可以看到，每一列是一家公司，每一行是時間點，值是股價(大概做過一些調整了，所以有正有負，我們可以不用管他，就當是股價即可)
如果我今天要做的分群，是對絕對的數值做分群，那我就直接用這張表分群就好.
但如果我今天是想對 “走勢” 做分群，那我會希望對 “列” 做標準化。
- 舉例來說，台積電的股價變化是 600, 580, 600, 620, 640，啟基是 60, 58, 60, 62, 64。
- 那從 “走勢” 來看，台積跟啟基走勢是一樣的，應該被分為一群，但如果直接做 kmeans，就再見了，因為光 600 和 60 的距離就很遠。
- 另外，台積股價的變化是 -20, 20, 20, 20; 啟基是 -2, 2, 2, 2，這個變動差距也不同，但如果改成看變化百分比(把股價放分母，變化當分子)，那兩邊就又差不多了.
- 所以，我如果先對列做標準化，那兩個公司的數值就都變成 [-0.39, -1.37, -0.39, 0.58, 1.56]，一模模一樣樣，euclidean distance 變成 0，分群時一定放在一塊兒
所以，這一個例子，我們就要對 “列” 做標準化，那就要用到 Normalizer 這個 preprocessor:

from sklearn.preprocessing import Normalizer
from sklearn.cluster import KMeans
from sklearn.pipeline import Pipeline, make_pipeline

# Create a normalizer: normalizer
normalizer = Normalizer()

# Create a KMeans model with 10 clusters: kmeans
kmeans = KMeans(n_clusters=10)

# Make a pipeline chaining normalizer and kmeans: pipeline
pipeline = make_pipeline(normalizer, kmeans)

# Fit pipeline to the daily price movements
pipeline.fit(movements)

Pipeline(steps=[('normalizer', Normalizer()),
                ('kmeans', KMeans(n_clusters=10))])

# Predict the cluster labels: labels
labels = pipeline.predict(movements)

# Create a DataFrame aligning labels and companies: df
df = pd.DataFrame({'labels': labels, 
                   'companies': movements.index})

# Display df sorted by cluster label
df.sort_values(["labels"])

	labels	companies
20	0	Home Depot
29	1	Lookheed Martin
36	1	Northrop Grumman
4	1	Boeing
58	2	Xerox
16	2	General Electrics
0	2	Apple
33	3	Microsoft
51	3	Texas instruments
50	3	Taiwan Semiconductor Manufacturing
47	3	Symantec
35	3	Navistar
32	3	3M
31	3	McDonalds
30	3	MasterCard
2	3	Amazon
24	3	Intel
23	3	IBM
3	3	American express
59	3	Yahoo
8	3	Caterpillar
17	3	Google/Alphabet
11	3	Cisco
13	3	DuPont de Nemours
14	3	Dell
7	4	Canon
45	4	Sony
48	4	Toyota
15	4	Ford
34	4	Mitsubishi
21	4	Honda
22	4	HP
9	5	Colgate-Palmolive
28	5	Coca Cola
38	5	Pepsi
52	6	Unilever
46	6	Sanofi-Aventis
43	6	SAP
42	6	Royal Dutch Shell
19	6	GlaxoSmithKline
6	6	British American Tobacco
37	6	Novartis
49	6	Total
57	7	Exxon
41	7	Philip Morris
44	7	Schlumberger
12	7	Chevron
53	7	Valero Energy
10	7	ConocoPhillips
55	8	Wells Fargo
18	8	Goldman Sachs
1	8	AIG
26	8	JPMorgan Chase
5	8	Bank of America
27	9	Kimberly-Clark
54	9	Walgreen
25	9	Johnson & Johnson
56	9	Wal-Mart
40	9	Procter Gamble
39	9	Pfizer

My sample book

Clustering

Contents

14. Clustering¶

14.1. K-Means¶

14.1.1. toy-example (iris)¶

14.1.2. stock movement¶

	SepalLengthCm	SepalWidthCm	PetalLengthCm	PetalWidthCm	Species
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

	SepalLengthCm	SepalWidthCm	PetalLengthCm	PetalWidthCm	Species
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

	SepalLengthCm	SepalWidthCm	PetalLengthCm	PetalWidthCm	Species
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0